Draw First Couple Level of the Search Tree
Let us consider the below traversals:
Inorder sequence: D B E A F C
Preorder sequence: A B D E C F
In a Preorder sequence, the leftmost element is the root of the tree. So we know 'A' is the root for given sequences. By searching 'A' in the Inorder sequence, we can find out all elements on the left side of 'A' is in the left subtree, and elements on right in the right subtree. So we know the below structure now.
A / \ / \ D B E F C
We recursively follow the above steps and get the following tree.
A / \ / \ B C / \ / / \ / D E F
Algorithm: buildTree()
1) Pick an element from Preorder. Increment a Preorder Index Variable (preIndex in below code) to pick the next element in the next recursive call.
2) Create a new tree node tNode with the data as the picked element.
3) Find the picked element's index in Inorder. Let the index be inIndex.
4) Call buildTree for elements before inIndex and make the built tree as a left subtree of tNode.
5) Call buildTree for elements after inIndex and make the built tree as a right subtree of tNode.
6) return tNode.
C++
#include <bits/stdc++.h>
using namespace std;
class node
{
public :
char data;
node* left;
node* right;
};
int search( char arr[], int strt, int end, char value);
node* newNode( char data);
node* buildTree( char in[], char pre[], int inStrt, int inEnd)
{
static int preIndex = 0;
if (inStrt > inEnd)
return NULL;
node* tNode = newNode(pre[preIndex++]);
if (inStrt == inEnd)
return tNode;
int inIndex = search(in, inStrt, inEnd, tNode->data);
tNode->left = buildTree(in, pre, inStrt, inIndex - 1);
tNode->right = buildTree(in, pre, inIndex + 1, inEnd);
return tNode;
}
int search( char arr[], int strt, int end, char value)
{
int i;
for (i = strt; i <= end; i++)
{
if (arr[i] == value)
return i;
}
}
node* newNode( char data)
{
node* Node = new node();
Node->data = data;
Node->left = NULL;
Node->right = NULL;
return (Node);
}
void printInorder(node* node)
{
if (node == NULL)
return ;
printInorder(node->left);
cout<<node->data<< " " ;
printInorder(node->right);
}
int main()
{
char in[] = { 'D' , 'B' , 'E' , 'A' , 'F' , 'C' };
char pre[] = { 'A' , 'B' , 'D' , 'E' , 'C' , 'F' };
int len = sizeof (in) / sizeof (in[0]);
node* root = buildTree(in, pre, 0, len - 1);
cout << "Inorder traversal of the constructed tree is \n" ;
printInorder(root);
}
C
#include <stdio.h>
#include <stdlib.h>
struct node {
char data;
struct node* left;
struct node* right;
};
int search( char arr[], int strt, int end, char value);
struct node* newNode( char data);
struct node* buildTree( char in[], char pre[], int inStrt, int inEnd)
{
static int preIndex = 0;
if (inStrt > inEnd)
return NULL;
struct node* tNode = newNode(pre[preIndex++]);
if (inStrt == inEnd)
return tNode;
int inIndex = search(in, inStrt, inEnd, tNode->data);
tNode->left = buildTree(in, pre, inStrt, inIndex - 1);
tNode->right = buildTree(in, pre, inIndex + 1, inEnd);
return tNode;
}
int search( char arr[], int strt, int end, char value)
{
int i;
for (i = strt; i <= end; i++) {
if (arr[i] == value)
return i;
}
}
struct node* newNode( char data)
{
struct node* node = ( struct node*) malloc ( sizeof ( struct node));
node->data = data;
node->left = NULL;
node->right = NULL;
return (node);
}
void printInorder( struct node* node)
{
if (node == NULL)
return ;
printInorder(node->left);
printf ( "%c " , node->data);
printInorder(node->right);
}
int main()
{
char in[] = { 'D' , 'B' , 'E' , 'A' , 'F' , 'C' };
char pre[] = { 'A' , 'B' , 'D' , 'E' , 'C' , 'F' };
int len = sizeof (in) / sizeof (in[0]);
struct node* root = buildTree(in, pre, 0, len - 1);
printf ( "Inorder traversal of the constructed tree is \n" );
printInorder(root);
getchar ();
}
Java
class Node {
char data;
Node left, right;
Node( char item)
{
data = item;
left = right = null ;
}
}
class BinaryTree {
Node root;
static int preIndex = 0 ;
Node buildTree( char in[], char pre[], int inStrt, int inEnd)
{
if (inStrt > inEnd)
return null ;
Node tNode = new Node(pre[preIndex++]);
if (inStrt == inEnd)
return tNode;
int inIndex = search(in, inStrt, inEnd, tNode.data);
tNode.left = buildTree(in, pre, inStrt, inIndex - 1 );
tNode.right = buildTree(in, pre, inIndex + 1 , inEnd);
return tNode;
}
int search( char arr[], int strt, int end, char value)
{
int i;
for (i = strt; i <= end; i++) {
if (arr[i] == value)
return i;
}
return i;
}
void printInorder(Node node)
{
if (node == null )
return ;
printInorder(node.left);
System.out.print(node.data + " " );
printInorder(node.right);
}
public static void main(String args[])
{
BinaryTree tree = new BinaryTree();
char in[] = new char [] { 'D' , 'B' , 'E' , 'A' , 'F' , 'C' };
char pre[] = new char [] { 'A' , 'B' , 'D' , 'E' , 'C' , 'F' };
int len = in.length;
Node root = tree.buildTree(in, pre, 0 , len - 1 );
System.out.println( "Inorder traversal of constructed tree is : " );
tree.printInorder(root);
}
}
Python3
class Node:
def __init__( self , data):
self .data = data
self .left = None
self .right = None
def buildTree(inOrder, preOrder, inStrt, inEnd):
if (inStrt > inEnd):
return None
tNode = Node(preOrder[buildTree.preIndex])
buildTree.preIndex + = 1
if inStrt = = inEnd :
return tNode
inIndex = search(inOrder, inStrt, inEnd, tNode.data)
tNode.left = buildTree(inOrder, preOrder, inStrt, inIndex - 1 )
tNode.right = buildTree(inOrder, preOrder, inIndex + 1 , inEnd)
return tNode
def search(arr, start, end, value):
for i in range (start, end + 1 ):
if arr[i] = = value:
return i
def printInorder(node):
if node is None :
return
printInorder(node.left)
print (node.data,end = ' ' )
printInorder(node.right)
inOrder = [ 'D' , 'B' , 'E' , 'A' , 'F' , 'C' ]
preOrder = [ 'A' , 'B' , 'D' , 'E' , 'C' , 'F' ]
buildTree.preIndex = 0
root = buildTree(inOrder, preOrder, 0 , len (inOrder) - 1 )
print ( "Inorder traversal of the constructed tree is" )
printInorder(root)
C#
using System;
public class Node {
public char data;
public Node left, right;
public Node( char item)
{
data = item;
left = right = null ;
}
}
class GFG {
public Node root;
public static int preIndex = 0;
public virtual Node buildTree( char [] arr, char [] pre,
int inStrt, int inEnd)
{
if (inStrt > inEnd) {
return null ;
}
Node tNode = new Node(pre[preIndex++]);
if (inStrt == inEnd) {
return tNode;
}
int inIndex = search(arr, inStrt,
inEnd, tNode.data);
tNode.left = buildTree(arr, pre, inStrt, inIndex - 1);
tNode.right = buildTree(arr, pre, inIndex + 1, inEnd);
return tNode;
}
public virtual int search( char [] arr, int strt,
int end, char value)
{
int i;
for (i = strt; i <= end; i++) {
if (arr[i] == value) {
return i;
}
}
return i;
}
public virtual void printInorder(Node node)
{
if (node == null ) {
return ;
}
printInorder(node.left);
Console.Write(node.data + " " );
printInorder(node.right);
}
public static void Main( string [] args)
{
GFG tree = new GFG();
char [] arr = new char [] { 'D' , 'B' , 'E' , 'A' , 'F' , 'C' };
char [] pre = new char [] { 'A' , 'B' , 'D' , 'E' , 'C' , 'F' };
int len = arr.Length;
Node root = tree.buildTree(arr, pre, 0, len - 1);
Console.WriteLine( "Inorder traversal of "
+ "constructed tree is : " );
tree.printInorder(root);
}
}
Javascript
<script>
class Node
{
constructor(item)
{
this .data = item;
this .left = this .right = null ;
}
}
let root;
let preIndex = 0;
function buildTree(In, pre, inStrt, inEnd)
{
if (inStrt > inEnd)
return null ;
let tNode = new Node(pre[preIndex++]);
if (inStrt == inEnd)
return tNode;
let inIndex = search(In, inStrt,
inEnd, tNode.data);
tNode.left = buildTree(In, pre, inStrt,
inIndex - 1);
tNode.right = buildTree(In, pre,
inIndex + 1,
inEnd);
return tNode;
}
function search(arr, strt, end, value)
{
let i;
for (i = strt; i <= end; i++)
{
if (arr[i] == value)
return i;
}
return i;
}
function printInorder(node)
{
if (node == null )
return ;
printInorder(node.left);
document.write(node.data + " " );
printInorder(node.right);
}
let In = [ 'D ', ' B ', ' E ', ' A ', ' F ', ' C ' ];
let pre = [ ' A ', ' B ', ' D ', ' E ', ' C ', ' F'];
let len = In.length;
root = buildTree(In, pre, 0, len - 1);
document.write( "Inorder traversal of " +
"constructed tree is : <br>" );
printInorder(root);
</script>
Output:
Inorder traversal of the constructed tree is D B E A F C
Time Complexity: O(n^2). The worst case occurs when the tree is left-skewed. Example Preorder and Inorder traversals for worst-case are {A, B, C, D} and {D, C, B, A}.
Efficient Approach :
We can optimize the above solution using hashing (unordered_map in C++ or HashMap in Java). We store indexes of inorder traversal in a hash table. So that search can be done O(1) time.
C++
#include <bits/stdc++.h>
using namespace std;
struct Node {
char data;
struct Node* left;
struct Node* right;
};
struct Node* newNode( char data)
{
struct Node* node = new Node;
node->data = data;
node->left = node->right = NULL;
return (node);
}
struct Node* buildTree( char in[], char pre[], int inStrt,
int inEnd, unordered_map< char , int >& mp)
{
static int preIndex = 0;
if (inStrt > inEnd)
return NULL;
char curr = pre[preIndex++];
struct Node* tNode = newNode(curr);
if (inStrt == inEnd)
return tNode;
int inIndex = mp[curr];
tNode->left = buildTree(in, pre, inStrt, inIndex - 1, mp);
tNode->right = buildTree(in, pre, inIndex + 1, inEnd, mp);
return tNode;
}
struct Node* buldTreeWrap( char in[], char pre[], int len)
{
unordered_map< char , int > mp;
for ( int i = 0; i < len; i++)
mp[in[i]] = i;
return buildTree(in, pre, 0, len - 1, mp);
}
void printInorder( struct Node* node)
{
if (node == NULL)
return ;
printInorder(node->left);
printf ( "%c " , node->data);
printInorder(node->right);
}
int main()
{
char in[] = { 'D' , 'B' , 'E' , 'A' , 'F' , 'C' };
char pre[] = { 'A' , 'B' , 'D' , 'E' , 'C' , 'F' };
int len = sizeof (in) / sizeof (in[0]);
struct Node* root = buldTreeWrap(in, pre, len);
printf ( "Inorder traversal of the constructed tree is \n" );
printInorder(root);
}
Java
import java.io.*;
import java.util.*;
class Node
{
char data;
Node left,right;
Node( char item)
{
data = item;
left = right = null ;
}
}
class Tree
{
public static Node root;
static HashMap<Character,Integer> mp = new HashMap<>();
static int preIndex = 0 ;
public static Node buildTree( char [] in, char [] pre, int inStrt, int inEnd)
{
if (inStrt > inEnd)
{
return null ;
}
char curr = pre[preIndex++];
Node tNode;
tNode = new Node(curr);
if (inStrt == inEnd)
{
return tNode;
}
int inIndex = mp.get(curr);
tNode.left = buildTree(in, pre, inStrt, inIndex - 1 );
tNode.right = buildTree(in, pre, inIndex + 1 , inEnd);
return tNode;
}
public static Node buldTreeWrap( char [] in, char [] pre, int len)
{
for ( int i = 0 ; i < len; i++)
{
mp.put(in[i], i);
}
return buildTree(in, pre, 0 , len - 1 );
}
static void printInorder(Node node)
{
if (node == null )
{
return ;
}
printInorder(node.left);
System.out.print(node.data + " " );
printInorder(node.right);
}
public static void main (String[] args)
{
char [] in = { 'D' , 'B' , 'E' , 'A' , 'F' , 'C' };
char [] pre = { 'A' , 'B' , 'D' , 'E' , 'C' , 'F' };
int len = in.length;
Tree.root=buldTreeWrap(in, pre, len);
System.out.println( "Inorder traversal of the constructed tree is" );
printInorder(root);
}
}
Python3
class Node:
def __init__( self , x):
self .data = x
self .left = None
self .right = None
def buildTree(inn, pre, inStrt, inEnd):
global preIndex, mp
if (inStrt > inEnd):
return None
curr = pre[preIndex]
preIndex + = 1
tNode = Node(curr)
if (inStrt = = inEnd):
return tNode
inIndex = mp[curr]
tNode.left = buildTree(inn, pre, inStrt,
inIndex - 1 )
tNode.right = buildTree(inn, pre, inIndex + 1 ,
inEnd)
return tNode
def buldTreeWrap(inn, pre, lenn):
global mp
for i in range (lenn):
mp[inn[i]] = i
return buildTree(inn, pre, 0 , lenn - 1 )
def printInorder(node):
if (node = = None ):
return
printInorder(node.left)
print (node.data, end = " " )
printInorder(node.right)
if __name__ = = '__main__' :
mp = {}
preIndex = 0
inn = [ 'D' , 'B' , 'E' , 'A' , 'F' , 'C' ]
pre = [ 'A' , 'B' , 'D' , 'E' , 'C' , 'F' ]
lenn = len (inn)
root = buldTreeWrap(inn, pre,lenn)
print ( "Inorder traversal of "
"the constructed tree is" )
printInorder(root)
C#
using System;
using System.Collections.Generic;
public class Node
{
public char data;
public Node left, right;
public Node( char d)
{
data = d;
left = right = null ;
}
}
public class Tree
{
public static Node root;
static Dictionary< char , int > mp = new Dictionary< char , int >();
static int preIndex = 0;
static Node buildTree( char [] In, char [] pre,
int inStrt, int inEnd)
{
if (inStrt > inEnd)
{
return null ;
}
char curr = pre[preIndex++];
Node tNode;
tNode = new Node(curr);
if (inStrt == inEnd)
{
return tNode;
}
int inIndex = mp[curr];
tNode.left = buildTree(In, pre, inStrt, inIndex - 1);
tNode.right = buildTree(In, pre, inIndex + 1, inEnd);
return tNode;
}
public static Node buldTreeWrap( char [] In, char [] pre, int len)
{
for ( int i = 0; i < len; i++)
{
mp.Add(In[i], i);
}
return buildTree(In, pre, 0, len - 1);
}
static void printInorder(Node node)
{
if (node == null )
{
return ;
}
printInorder(node.left);
Console.Write(node.data + " " );
printInorder(node.right);
}
static public void Main (){
char [] In = { 'D' , 'B' , 'E' , 'A' , 'F' , 'C' };
char [] pre = { 'A' , 'B' , 'D' , 'E' , 'C' , 'F' };
int len = In.Length;
Tree.root = buldTreeWrap(In, pre, len);
Console.WriteLine( "Inorder traversal of the constructed tree is" );
printInorder(Tree.root);
}
}
Output:
Inorder traversal of the constructed tree is D B E A F C
Time Complexity : O(n)
Another approach :
Use the fact that InOrder traversal is Left-Root-Right and PreOrder traversal is Root-Left-Right. Also, the first node in the PreOrder traversal is always the root node and the first node in the InOrder traversal is the leftmost node in the tree.
Maintain two data structures: Stack (to store the path we visited while traversing PreOrder array) and Set (to maintain the node in which the next right subtree is expected).
1. Do below until you reach the leftmost node.
Keep creating the nodes from the PreOrder traversal
If the stack's topmost element is not in the set, link the created node to the left child of the stack's topmost element (if any), without popping the element.
Else link the created node to the right child of the stack's topmost element. Remove the stack's topmost element from the set and the stack.
Push the node to a stack.

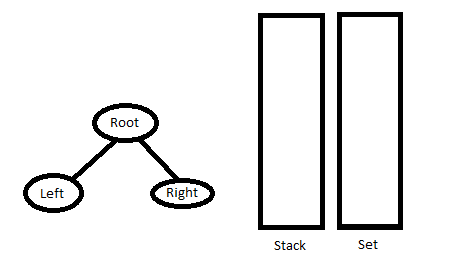
2. Keep popping the nodes from the stack until either the stack is empty, or the topmost element of the stack compares to the current element of InOrder traversal. Once the loop is over, push the last node back into the stack and into the set.
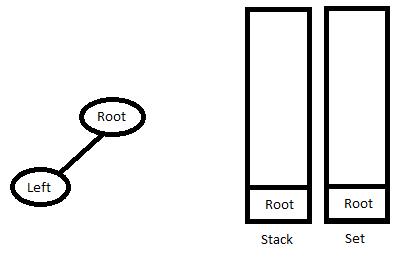
3. Goto Step 1.
C++
#include<bits/stdc++.h>
using namespace std;
class TreeNode
{
public :
int val;
TreeNode* left;
TreeNode* right;
TreeNode( int x) { val = x; }
};
set<TreeNode*> s;
stack<TreeNode*> st;
TreeNode* buildTree( int preorder[], int inorder[], int n)
{
TreeNode* root = NULL;
for ( int pre = 0, in = 0; pre < n;)
{
TreeNode* node = NULL;
do
{
node = new TreeNode(preorder[pre]);
if (root == NULL)
{
root = node;
}
if (st.size() > 0)
{
if (s.find(st.top()) != s.end())
{
s.erase(st.top());
st.top()->right = node;
st.pop();
}
else
{
st.top()->left = node;
}
}
st.push(node);
} while (preorder[pre++] != inorder[in] && pre < n);
node = NULL;
while (st.size() > 0 && in < n &&
st.top()->val == inorder[in])
{
node = st.top();
st.pop();
in++;
}
if (node != NULL)
{
s.insert(node);
st.push(node);
}
}
return root;
}
void printInorder(TreeNode* node)
{
if (node == NULL)
return ;
printInorder(node->left);
cout << node->val << " " ;
printInorder(node->right);
}
int main()
{
int in[] = { 9, 8, 4, 2, 10, 5, 10, 1, 6, 3, 13, 12, 7 };
int pre[] = { 1, 2, 4, 8, 9, 5, 10, 10, 3, 6, 7, 12, 13 };
int len = sizeof (in)/ sizeof ( int );
TreeNode *root = buildTree(pre, in, len);
printInorder(root);
return 0;
}
Java
import java.util.*;
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode( int x) { val = x; }
}
class BinaryTree {
static Set<TreeNode> set = new HashSet<>();
static Stack<TreeNode> stack = new Stack<>();
public TreeNode buildTree( int [] preorder, int [] inorder)
{
TreeNode root = null ;
for ( int pre = 0 , in = 0 ; pre < preorder.length;) {
TreeNode node = null ;
do {
node = new TreeNode(preorder[pre]);
if (root == null ) {
root = node;
}
if (!stack.isEmpty()) {
if (set.contains(stack.peek())) {
set.remove(stack.peek());
stack.pop().right = node;
}
else {
stack.peek().left = node;
}
}
stack.push(node);
} while (preorder[pre++] != inorder[in] && pre < preorder.length);
node = null ;
while (!stack.isEmpty() && in < inorder.length &&
stack.peek().val == inorder[in]) {
node = stack.pop();
in++;
}
if (node != null ) {
set.add(node);
stack.push(node);
}
}
return root;
}
void printInorder(TreeNode node)
{
if (node == null )
return ;
printInorder(node.left);
System.out.print(node.val + " " );
printInorder(node.right);
}
public static void main(String args[])
{
BinaryTree tree = new BinaryTree();
int in[] = new int [] { 9 , 8 , 4 , 2 , 10 , 5 , 10 , 1 , 6 , 3 , 13 , 12 , 7 };
int pre[] = new int [] { 1 , 2 , 4 , 8 , 9 , 5 , 10 , 10 , 3 , 6 , 7 , 12 , 13 };
int len = in.length;
TreeNode root = tree.buildTree(pre, in);
tree.printInorder(root);
}
}
Python3
class TreeNode:
def __init__( self , x):
self .val = x
self .left = None
self .right = None
s = set ()
st = []
def buildTree(preorder, inorder, n):
root = None ;
pre = 0
in_t = 0
while pre < n:
node = None ;
while True :
node = TreeNode(preorder[pre])
if (root = = None ):
root = node;
if ( len (st) > 0 ):
if (st[ - 1 ] in s):
s.discard(st[ - 1 ]);
st[ - 1 ].right = node;
st.pop();
else :
st[ - 1 ].left = node;
st.append(node);
if pre> = n or preorder[pre] = = inorder[in_t]:
pre + = 1
break
pre + = 1
node = None ;
while ( len (st) > 0 and in_t < n and st[ - 1 ].val = = inorder[in_t]):
node = st[ - 1 ];
st.pop();
in_t + = 1
if (node ! = None ):
s.add(node);
st.append(node);
return root;
def printInorder( node):
if (node = = None ):
return ;
printInorder(node.left);
print (node.val, end = " " );
printInorder(node.right);
if __name__ = = '__main__' :
in_t = [ 9 , 8 , 4 , 2 , 10 , 5 , 10 , 1 , 6 , 3 , 13 , 12 , 7 ]
pre = [ 1 , 2 , 4 , 8 , 9 , 5 , 10 , 10 , 3 , 6 , 7 , 12 , 13 ]
l = len (in_t)
root = buildTree(pre, in_t, l);
printInorder(root);
C#
using System;
using System.Collections.Generic;
public class TreeNode
{
public int val;
public TreeNode left;
public TreeNode right;
public TreeNode( int x) { val = x; }
}
class GFG
{
static HashSet<TreeNode> set = new HashSet<TreeNode>();
static Stack<TreeNode> stack = new Stack<TreeNode>();
public TreeNode buildTree( int [] preorder, int [] inorder)
{
TreeNode root = null ;
for ( int pre = 0, iN = 0; pre < preorder.Length;)
{
TreeNode node = null ;
do {
node = new TreeNode(preorder[pre]);
if (root == null )
{
root = node;
}
if (stack.Count != 0)
{
if ( set .Contains(stack.Peek()))
{
set .Remove(stack.Peek());
stack.Pop().right = node;
}
else
{
stack.Peek().left = node;
}
}
stack.Push(node);
} while (preorder[pre++] != inorder[iN] &&
pre < preorder.Length);
node = null ;
while (stack.Count != 0 && iN < inorder.Length &&
stack.Peek().val == inorder[iN])
{
node = stack.Pop();
iN++;
}
if (node != null )
{
set .Add(node);
stack.Push(node);
}
}
return root;
}
void printInorder(TreeNode node)
{
if (node == null )
return ;
printInorder(node.left);
Console.Write(node.val + " " );
printInorder(node.right);
}
public static void Main(String []args)
{
GFG tree = new GFG();
int []iN = new int [] { 9, 8, 4, 2, 10, 5, 10,
1, 6, 3, 13, 12, 7 };
int []pre = new int [] { 1, 2, 4, 8, 9, 5, 10,
10, 3, 6, 7, 12, 13 };
int len = iN.Length;
TreeNode root = tree.buildTree(pre, iN);
tree.printInorder(root);
}
}
Javascript
<script>
class TreeNode
{
constructor(x) {
this .val = x;
this .left = null ;
this .right = null ;
}
}
let set = new Set();
let stack = [];
function buildTree(preorder,inorder)
{
let root = null ;
for (let pre = 0,In=0; pre < preorder.length;) {
let node = null ;
do {
node = new TreeNode(preorder[pre]);
if (root == null ) {
root = node;
}
if (stack.length!=0) {
if (set.has(stack[stack.length-1])) {
set. delete (stack[stack.length-1]);
stack.pop().right = node;
}
else {
stack[stack.length-1].left = node;
}
}
stack.push(node);
} while (preorder[pre++] != inorder[In] && pre < preorder.length);
node = null ;
while (stack.length!=0 && In < inorder.length &&
stack[stack.length-1].val == inorder[In]) {
node = stack.pop();
In++;
}
if (node != null ) {
set.add(node);
stack.push(node);
}
}
return root;
}
function printInorder(node)
{
if (node == null )
return ;
printInorder(node.left);
document.write(node.val + " " );
printInorder(node.right);
}
let In=[9, 8, 4, 2, 10, 5, 10, 1, 6, 3, 13, 12, 7 ];
let pre=[1, 2, 4, 8, 9, 5, 10, 10, 3, 6, 7, 12, 13 ];
let len = In.length;
let root=buildTree(pre, In);
printInorder(root);
</script>
Output:
9 8 4 2 10 5 10 1 6 3 13 12 7
Construct a Binary Tree from Postorder and Inorder
Source: https://www.geeksforgeeks.org/construct-tree-from-given-inorder-and-preorder-traversal/
0 Response to "Draw First Couple Level of the Search Tree"
Publicar un comentario